Animation of Water Waves Generated by External Perturbation
This is a team project.
In this project, we use the program to model water animation that can be run in real-time applications with modest hardware while still preserves realistic visual appearance.
We plan to approach the problem by using dynamic normal maps to simulate visual appearance of water waves. Our project will include following components:
§ The program is base on a sample code, we modified and added several features in the code.§
The whole project can be separated into several parts.
The first one is outline detection.
The simulated water waves should resemble outline of the object.
To generate the outline, the object will be projected onto water plane by orthogonal projection.

The second part is "Texture Coordinate Shifting". Here we use notion of height to present the wave. Three arrays(512x512) are used to store height value, which are named Previous, Current and Next. Previous and Current store height values of previous and current time frame. Height values in Next are computed based on Previous and Current and are used for texture coordinate shifting. In this project, we propagate waves for one unit. Each unit is assumed to be half cycle of underlying oscillated waves. Then the height can be expressed by:
Now we can compute height values of each coordinate in Next from values in Previous and Current. A damping value is also used to allow waves to slowly calm down.
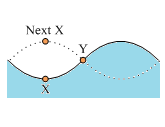
After this, we perform texture coordinate shifting by using the height value in Next. Shifting in x axis, or u axis in texture terminology, is determined by difference of height values between above and below neighbors; y axis, or v axis, by difference between right and left neighbors. we have tried other combinations, such as u axis shifting by right and left neighbors, and the visual effects are the same to us. Thus we argue that the fact of texture shifting is much more important than shifting direction. Finally, arrays are swapped as preparation for following time frame. Here is the result:

In addition, we also test the ripple effect. We simulates the effect of bouncing back when waves encounter boundary or obstacles. The basic idea for bouncing is that when boundary is encountered, the next height value should be the same as previous value with respect to inference of boundary neighbor. Also, the ripple can be affected by different shape of obstacles.

At last, we also compare the efficency and effect between using multiple polygons and flat plane. Instead of transforming height values into texture coordinate shifting, we implement a program that uses height values to construct polygons for our water waves. This model results in more than a half million triangles instead of two compared to water plane model. Not surprising, frame per second drops from more than 60 to 5 or less on a laptop with Intel Core 2 Duo 2.4 GHz and NVIDA GeForce 8400M GS.

Demo video :
P.S. The program is base on a sample code, we modified and added several features in the code .
reference data :
1. Gergely Klar, "Flow Simulation using Obstacle Dependent Grids," CESCG, 2008.
2. Realistic Sailing a Virtual Ocean, see link
3. Normal Mapping - Add depth to your flat surfaces with normal mapping, see link
4. Teng-See Loke, Daniel Tan, Hock-Soon Seah, and Meng-Hwa Er, "Rendering Fireworks Displays," IEEE Computer Graphics and Applications, IEEE, vol. 12, no. 3, May 1992, 33-43.
5. �^���, 3Dø�ϵ{���]�p�G�ϥ�Direct3D�POpenGL 2.0